←前のページ 次のページ→
4.スクリプトの説明〜”三角関数計算”
次は、1番難しい
”三角関数計算”のスクリプトです。今回はあとで図を載せます。
前にも言いましたがこのスクリプトだけSmalltalkです。実は難しいので自分一人ではやっていません。
さて、説明に入っていきますが、そもそも三角関数とは何なのか。それは、次のような図で表すことができます。
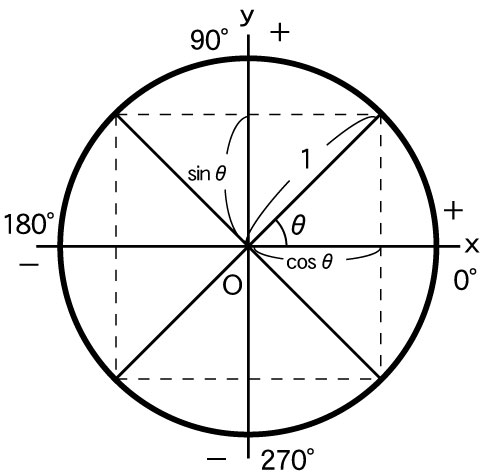
※x、yというのはそれぞれx軸、y軸のことです。
そして、図の円の半径は1で、いつでも+です。でも、図にある
sinθと
cosθという値は、
線のθ値によって+か-かが変わります。(下の表を参考にしてください)
| 線のθ値が |
0°〜 90°のとき |
sinθは+で、cosθも+ |
| 90°〜 180°のとき |
sinθは+で、cosθは- |
| 180°〜 270°のとき |
sinθは-で、cosθも- |
| 270°〜 0°のとき |
sinθは-で、cosθは+ |
これをもとにして、実際にSqueakでの座標計算に当てはめていくと、次の図のようになります。
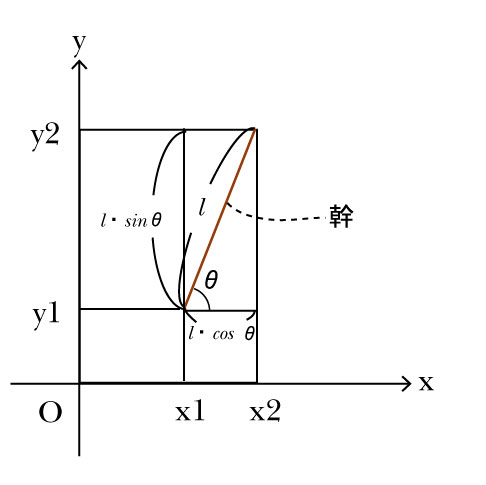
※x、yというのは前の図と同じくx軸、y軸のことで、x1、x2、y1、y2というのは座標のことを表しています。
そして、幹は前の図の半径の線分に当てはまります。
x1とy1の座標はわかっています。(幹のx座標とy座標のことなので)そして次に、x2とy2の座標を求めます。
その求め方は、幹の長さを
l (エル)として次のような式で求めることができます。
| x2を求める |
x2 - x1 = l cosθ より x2 = x1 + l cosθ |
| y2を求める |
y2 - y1 = l sinθ より y2 = y1 + l sinθ |
という式です。この式を使うと、幹がどんな方向を向いていても同じ式で求めることができます。
あとは、求めたx2、y2の値に1/3や2/3をかけることによって、次の枝の生える位置が求められます。
(”枝一本目”では1/3、”枝二本目”では2/3、”枝三本目”ではそのままの値でスクリプトを作っています)
Smalltalkでは次のように書いています。
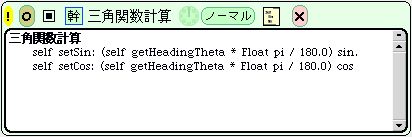
わかりやすく書くと、
sinの値 = 向きの値 × π(円周率) ÷ 180
cosの値 = 向きの値 × π ÷ 180 |
となります。ここで、”π÷180”を掛けているのは角度をラジアンに変換するためです。
Smalltalkでは向きの値は
”getHeadingTheta”、πは
”Float pi”と表します。
どうやって調べたかというと、例えば次のようにします。
まず図のようにタイルスクリプトで”向きの値”のタイルを入れたスクリプトを作ります。
作ったら、タイルスクリプトとSmalltalkスクリプトの切り替えボタンを押します。

すると次の図のようになります。
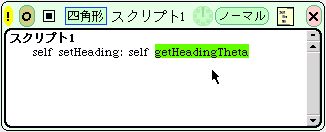
これは次のように読み替えることができます。
| self(自分の) setHeading:(向きは) self(自分の) getHeadingTheta(向きの値) |
という感じです。
P.S: これを作った後に”Float pi” について調べていると、
”degreeCos”と
”degreeSin”というメソッドがありました。
これを使えば”π÷180”を掛ける必要がなくなります。もうちょっと楽にできたかも。(^^;)
次のページでは、”枝を半分にする”スクリプトの説明をします。
←前のページ 次のページ→





