とある京大生のホームページのTOP >
数学全般 >
オイラーの公式
オイラーの公式
今日は、オイラーの公式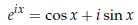 の導き方を紹介します。
の導き方を紹介します。
[導き方]
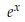 の定義から
の定義から
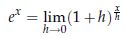
これを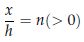 として変形すると
として変形すると
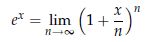 だから
だから 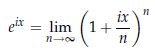
nは∞にもっていくので、自然数に限定して考える。
ここで、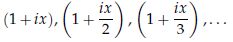 という数列
という数列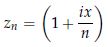 を考え、その後
を考え、その後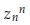 を考えることにする。・・・・・・
を考えることにする。・・・・・・
といった感じで、その後は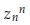 の偏角と大きさ(絶対値)を求めることによって公式が導かれます。
の偏角と大きさ(絶対値)を求めることによって公式が導かれます。
詳しくはこちらのPDFファイルをどうぞ。
※ この導き方は、以前紹介した「世にも美味しい数学」 (古川昭夫・稲垣裕子 著 日本実業出版社)という本を参考にしたものですが、以前読んだときはよく理解できなかったのが最近やっと理解できたので紹介しました。
おはようございます。
ちょっと質問ですが、数式はTEXで書いているのですか?
投稿者: 271828 | 2007年4月 9日 05:36
>> 271828さん
コメントありがとうございます。
数式はTEXで書いて、dvipdfmxを使ってPDFファイルにしています。なお、HTMLの方に載せている数式は、作ったPDFを開いておいて、Winshotで画像(JPG)にしています。
ブログの方も見させて頂きました。画像が多いのでとても見やすくなっていると思います。また、僕は数学のことを書いてそこで終わってしまっていますが、271828さんはまず物理的な観点から物を見て、そこで数学の知識を使っているのですごいと思います。
投稿者: とある中学生 | 2007年4月 9日 12:39
やはりTeXですか。
どうもこの年になると面倒なことを覚えるのが億劫になります。美しさでは絶対TeXなんですがねぇ。
私のブログは滑り台がメインコンテンツのはずですが、最近「対数ブログ」になりつつあります。需要があるということでしょうか。
土曜日に円形計算尺が届きましたが、実に良いです。これをネタにまた書きますのでご期待下さい。
それからメールアドレスを書かせるのは止めたほうが良いですね。皆スパムメールにはうんざりしていますから。
投稿者: 271828 | 2007年4月 9日 16:38
>> 271828さん
円形計算尺がどんなものなのかはよく知らないのですが、面白そうなので期待して待っています。
また、ご忠告に従って、メールアドレスの欄はなくすことにし、名前だけにしました。またご意見がありましたらコメントをお願いします。
投稿者: とある中学生 | 2007年4月 9日 22:38
おはよう
メールは書かなくても良いけれどURLは必要かもしれない。
ブログ村の科学ブログのサブカテゴリーに数学があります。トップの「数学放浪紀行」
http://science.blogmura.com/mathematics/
の管理人は中3ですね。3人しかエントリーしていないので最悪4位です。
登録も無料なのでどうですか、やってみては。
投稿者: 271828 | 2007年4月11日 06:14
はじめまして 質問です;
問1 乗積
Product[Sqrt[(-1+Cos[(2*k*Pi)/n])^2+Sin[(2*k*Pi)/n]^2],{k,1,n-1}] = n
の 証明を!
問2
Abs[Product[E^((2*k*Pi*I)/n)-1,{k, 1, n - 1}]]=n
の 証明を!
( 問1と問2は 同一ですが 独立した! シンプルな証明! を お願い致します!)
--------------------------------------
Γ函数を使う手法もあります。
投稿者: G | 2007年9月16日 11:07
そんなことやらなくてもテイラー展開をすれば
導けますよ
投稿者: テルル | 2007年11月21日 20:43
i like it. thanks a lot.
ICQ
投稿者: reureTiz | 2009年6月29日 14:28
Cool!
投稿者: Flash | 2009年7月 5日 18:16