数学全般
2009/01/12 A HAPPY NEW YEAR !!
明けましておめでとうございます（遅ッ！）。
約4ヶ月ぶりの更新です。このブログを読んで頂いている方々はどのような形で新年を迎えられたでしょうか。私は冬休みが始まったと同時に学校の冬季補習（4日間）が始まり、その後那須のキャンプ場にて「ゆく年くる年」を見ながら年を越し、課題に追われ、冬休み明けの実力テストでは数学で惨憺たる結果を残しながら現在に至ります。
さて、2009年の記念すべき第1回目の更新は、やはり数学に立ち返ろうではないかと。。。
このブログのコメントもよく書いてくださっている、271828さんに立体のパズルのようなものを貸して頂きましたので、それについて載せたいと思います。
見て頂ければお分かりかと思いますが、「サッカーボール」形のパズルとなっております。数学的？には切頂二十面体（truncated icosahedron）と言って、正二十面体の各頂点を切り落とすとこのような立体が出来上がります（ちなみに、切り口の正五角形をさらに大きくすると正十二面体が出来ます）。
内部の写真は撮らなかったのですが、小さな鉄球があって、それに磁石の付いたピースがくっ付けられるという構造になっています。
組むこと自体はそれほど難しくないのですが、赤・青・緑・黄色の4色で同じ色が隣り合わないように組むのが意外と難しいです。最初うまくいかなかったので次のような過程で考えたら成功しました。
＜Process＞
（1）まず、正五角形1つと、周りの正六角形5つを組んでしまう。どのような色の組み合わせであっても結局すべて同じことになるため。
（2）次に、その周囲の正五角形5つの色の組み合わせを適当に考える（1回失敗した）。
（3）あとは、絶対に当てはまる色のピースを組んでいきながら試行錯誤。
結局「試しながら出来ただけじゃん」とか言われそうですが、一応同じ失敗はしないように考えました。多分。
完成はしましたが、このピースの組み合わせは何通りの種類があるのだろうか・・・と素朴な疑問も。また、「四色問題」（分からない人はWikipediaで検索すれば出ると思います）なんてものがありましたが、球面上ではその定理は成り立つのだろうか、とパズルを組みながら思ったりしました。
何はともあれ、ブログネタをくださった271828さん、どうもありがとうございました。
------------------------------日時: 23:36 | コメント (2)
2008/09/12 数学コンテスト
5ヶ月以上更新をサボっておりました。久々に書き込みたいと思います。
夏休み中、学校で「高校生数学コンテスト」というものに参加しました。参加しました、というよりクラス全員で参加させられたという方が正しいでしょうか。
問題の形式としては、大問が6問あって、そのうち4問選択してすべて記述で解答します（定規やコンパス、電卓の使用は任意です）。制限時間は3時間（！）。なかなか長かったです。
それで、何だかんだ言いながら一応奨励賞を取ることができまして、今日は県庁でその表彰式があったわけです。表彰式の後、某大学の教授の方が1時間ほど講義をしてくださいました。ですが正直な話、「今何を求めようとしているのか」ということをはっきり言わないまま講義を進めていく（自分の世界・・・）ので、話の流れがつかめずサッパリでした。
実際の数学コンテストで、私が完答できた大問を1つ掲載しておきたいと思います。こちらのPDFファイルをご覧ください。（3）がやや難しいですが、f(n)の性質をうまく利用すれば解けると思います。ぜひ考えてみてください。
日時: 00:05 | コメント (0)
2007/07/01 余弦定理の導出
今日は、昨日紹介した数学の問題で使った余弦定理という定理の導出の仕方についてです。
※ これは、基本的な三角関数の知識があれば導くことができます。まあ、基本的な三角関数の知識がある人はたいてい余弦定理も知っていますが…。
詳しくはこちらのPDFファイルをどうぞ。
------------------------------日時: 20:57 | コメント (15)
2007/06/30 「コマネチ大学」より
このところずっと更新をサボっておりました。久々に載せます。
今回は、数学の問題を載せたいと思います。出題は、以前も紹介した「たけしのコマネチ大学数学科」という番組からです。下の図がその問題に関係します。
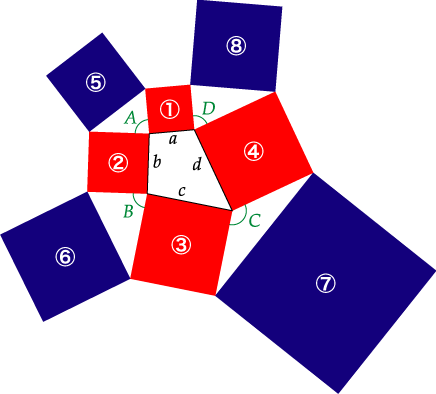
※ 自分にはよく分かりませんが、これはどうやら「ヒルベルト空間」というものと関連しているようです。
詳しくはこちらのPDFをどうぞ。
------------------------------日時: 16:02 | コメント (0)
2007/03/29 オイラーの公式
今日は、オイラーの公式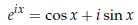
の導き方を紹介します。
［導き方］
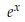の定義から
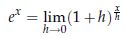
これを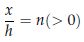
として変形すると
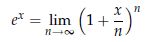だから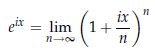 
nは∞にもっていくので、自然数に限定して考える。
ここで、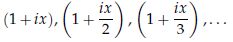
という数列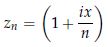
を考え、その後
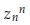を考えることにする。･･････
といった感じで、その後は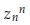の偏角と大きさ（絶対値）を求めることによって公式が導かれます。
詳しくはこちらのPDFファイルをどうぞ。
※ この導き方は、以前紹介した「世にも美味しい数学」 （古川昭夫・稲垣裕子 著 日本実業出版社）という本を参考にしたものですが、以前読んだときはよく理解できなかったのが最近やっと理解できたので紹介しました。
------------------------------日時: 16:57 | コメント (9)
2007/03/17 ライプニッツの公式
今日はライプニッツの公式を紹介します。
◎ ライプニッツの公式
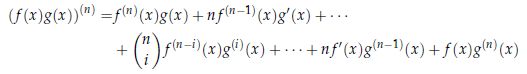
ただし、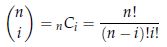
この公式を使えば、多項式の積のn回微分が簡単にできます。
［証明］
証明はPDF版のこちらをどうぞ。
日時: 17:58 | コメント (0)
2007/03/14 ド・モアブルの定理
すいません･･･しばらくサボっていたので、久々の更新になります。
今日は、ド・モアブルの定理を紹介したいと思います。有名なので知っている方も多いかとは思いますが･･･
◎ ド・モアブルの定理
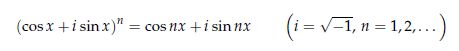
この定理の左辺のn乗を展開して実部･虚部を比較することで、三角関数のn倍角の公式を導くことができます。
［証明］
証明はPDF版のこちらをどうぞ。
日時: 22:37 | コメント (4)
2007/02/12 漸化式に関する話
数学の勉強をしていたら、3項の漸化式についてのことが書いてありました。途中の解説は書いてなくて、訳が分からなかったので、ネットで検索してみました。すると、それについて書かれたサイトがあったので、読んで理解することができました。
面白い問題なので、文書にまとめてみました。解説は、そのサイトの説明を自分がところどころ補足しています（問題はすべて文字式ですが、そのサイトは具体値で説明していたので）。こちらのファイル（PDF）を参照してください。
日時: 16:02 | コメント (1)
2007/01/31 ベクトルの問題
ベクトルの勉強をしていて、面白い問題があったので紹介します。面積比に関する問題で、結構有名な定理（らしい）の証明です。以下の画像（JPG）を参照してください（クリックすると拡大します）。時間の関係上手書きなので、もし見づらかったらごめんなさい。
日時: 23:04 | コメント (0)
2007/01/21 図形の問題
角度に関する図形の問題とその解法を紹介します。もしかしたら知っている人もいるかもしれません。こちらのファイル（PDF）を参照してください。
ファイル内にも書いてありますが、2つの解法を紹介していて、1つ目は小学生でも分かる解法、2つ目は複素平面を使った解法になっています。
なお、この問題は、以下の本（※）を読んで書いたものです。この本では2つ目の解法が紹介されています。少し難しい（分からないところもあります･･･）ですが、対話形式になっているので、読みやすく、とてもおもしろい本です。ぜひ読んでみてください。
※ 「世にも美味しい数学」 古川昭夫・稲垣裕子 著 日本実業出版社
------------------------------日時: 18:02 | コメント (0)
2007/01/17 連立方程式を行列式で
数年前、数学の本を読んでいて、行列式を使って連立方程式を解く方法が載っていました。それを参考にして、こんなものを作りました。PDFファイルです。以前作ったものなので、行列式の計算の仕方を忘れてしまいました（笑）。本を見返せば思い出すでしょうが。
------------------------------日時: 19:26 | コメント (1)
2007/01/11 微分方程式に取り組んでみた
少し前、微分方程式に取り組んで、こんなものを作ってみたので見てみてください。PDFファイルです。県の理科研究発表会で発表したものなので、プレゼンテーション用に作ってあります。
------------------------------日時: 23:10 | コメント (0)